Kuvittele itsesi sijoitusneuvontapalaveriin, aiheena varainhoito. Omaat 300 000 euroa ja haluat esimerkin sijoitussuunnitelmasta kuudelle vuodelle. Tavoitteesi on saada seitsemän prosentin nominaalituotto, joka vastaa matalan inflaation aikana karkeasti arvioiden kuuden prosentin reaalituottoa.
Private Bankingin asiakasvastaava printtaa sinulle paperin, jossa seitsemän prosentin tuotto piirtyy kauniin tasaisena kalliille paperille. Pääoma näyttää kaksinkertaistuvan vuosikymmenessä! Tämähän näyttää hyvältä. Innostut aritmeettisesta keskiarvosta ja olet vaarassa tehdä sijoituselämäsi suurimman virheen.
Koulun matematiikantunnilla päntätty keskiarvon laskenta (aritmeettinen) ei sovellu sijoittamiseen liittyvien tuottojen laskentaan, sillä se mittaa toisistaan riippumattomien lukujen keskiarvoa. Sijoittamisessa usean vuoden tuottojen laskennassa tulee huomioida niiden riippuvuus toisistaan.
Ei yrittäjänkään vuosituotot ole veljiä keskenään, vaan jonain vuosina tuottoja tulee enemmän, toisina vähemmän. Private Banking -asiakkaalle osuu pitkän matkan varrella takuuvarmasti tappiollisiakin vuosia. Tätä tuottojen keskihajontaa kutsutaan volatiliteetiksi.
Tuottojen keskiarvo tulee laskea geometrisesti, jolloin otetaan huomioon se fakta, että tuotot kertyvät vuosi toisensa perään toistensa päälle ”korkoa korolle”-mekanismilla. Eli sijoittajan saama tuotto ei ole yksittäisten vuosien keskiarvo vaan vuosittainen tulos, josta ponkaistaan taas eteenpäin seuraavan vuoden alussa.
Esimerkki valaisee
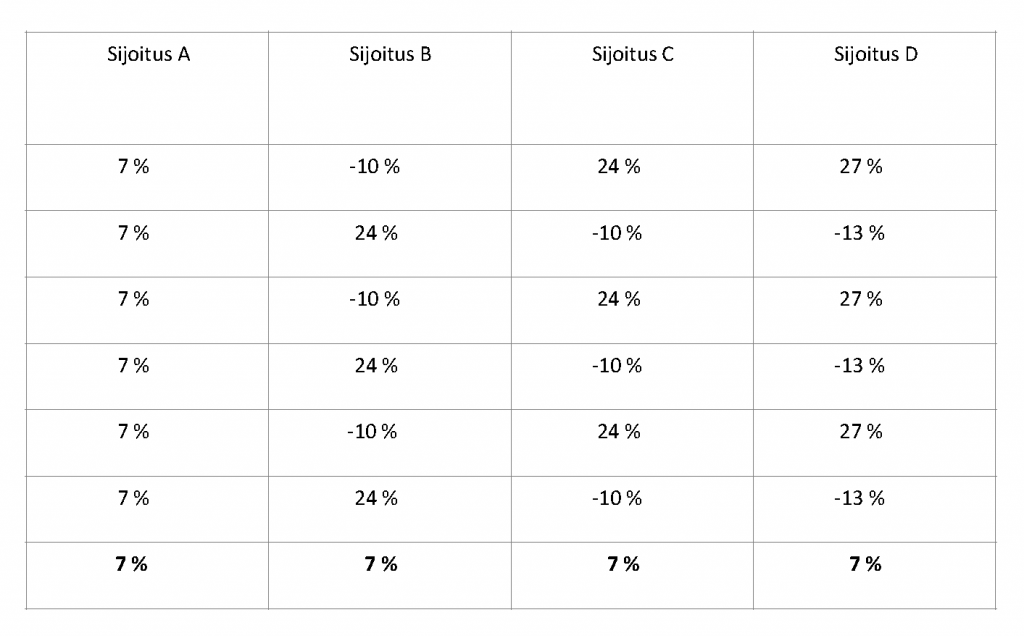
Sijoitus A (katso alla) kuvaa esimerkin sijoittajalle tarjottavaa aritmeettista laskelmaa. Täysin tasaisen vauhdin taulukolla myös geometrinen tuotto on seitsemän prosenttia. Sijoitus B ja C kuvaavat peilikuvina yksinkertaistettua, mutta jo monta astetta todellisempaa sijoitusmaisemaa. Sijoitus D kuvaa salkkua, jossa vuosituottojen heilunta on ollut kaikkein hurjinta.
Aritmeettiset tuotot
Miten esimerkit vaikuttavat geometrisiin tuottoihin ja sitä kautta todellisiin tuottoihin?
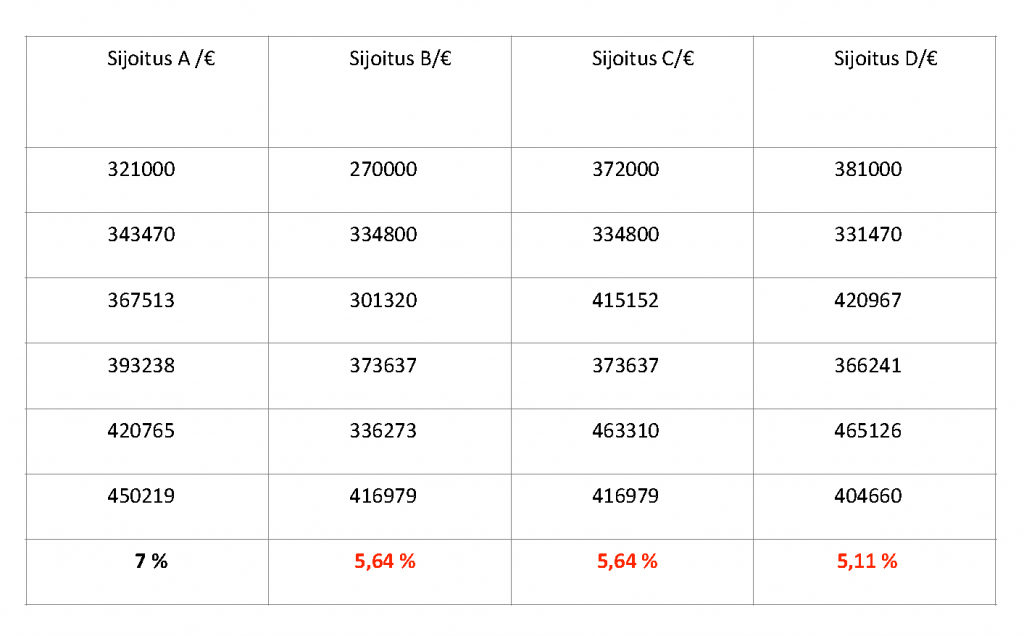
Sijoituksen aloittaminen voi osua nousu- tai laskuvuoteen. Sitä ei voi etukäteen kukaan tietää. Oleellista esimerkissä eivät ole prosentit sinänsä vaan niiden muutoksen vaikutus lopulliseen tuottoon. B:ssä ja C:ssä geometrinen tuotto jää 5,64 prosenttiin. 300 000 euroa kasvaakin 417 000 euroon eikä 450 000 euroon, jonka aritmeettinen käyrä antaa ymmärtää. Vaihtoehto D:ssä tuottoheilunta on voimakkainta, joka näkyy myös lopullisessa tuotossa.
Geometriset tuotot
Geometrinen tuotto edellä mainituille prosentuaalisille vuosituottoesimerkeille 300 000 euron aloitusvarallisuudella näyttää tältä:
Sijoittamiseen kiinteästi kuuluva tuottojen heilunta siis heikentää geometrisiä tuottoja. Esimerkeissä B ja C havaitaan, ettei käteen jäävää tuottoa laskiessa ole merkitystä, alkaako sijoitustaival voitollisesti tai tappiollisesti, jos muut parametrit pysyvät ennallaan. Esimerkki D paljastaa volatiliteettitason absoluuttisen kasvun vähentävän geometristä tuottoa.
Tutustu Private Banking toimintaamme täältä.
Pitkäjänteisen sijoittajan on syytä keskittyä geometrisen tuoton tarkasteluun, sillä aritmeettisella vuosituotolla ei osteta leipää kaupasta.